An exploratory mixed methods study using factor analysis and latent class analysis
I view our role as epidemiologists is to continually discover and learn methodologies that are applicable to public health (or clinical) problems, and I encourage my students to take methods courses rather than content area courses, to be generalists in their education, emerging from the program as applied methodologists. I've been particularly interested in learning qualitative study design, factor analysis, and latent class analysis for some time. Through my work at a local hospital with clinical fellows, I became involved in a project that allowed me to do all three at once.
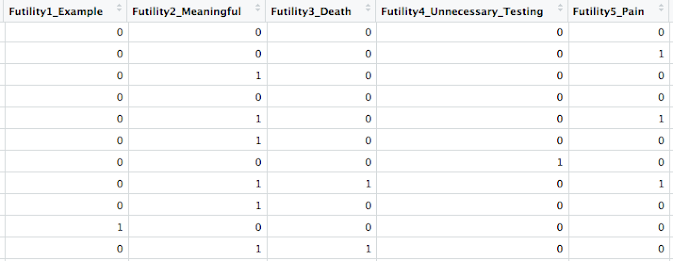
The project is centered around defining treatment futility in a clinical setting. The fellow recruited about 200 healthcare providers who work in an intensive care unit (ICU) at the hospital and through an open-ended question asked them "How do you define futility?" Based on the responses, this fellow and another physician came up with 13 thematic categories (constructs of futility) that captured the qualitative responses, where these categories were based on best-guesses and visual inspection of the answers. All 200 survey respondents were coded redundantly so we can assess kappa for inter-rater agreement between the two physicians, and each respondent's answer to the question fit under one or more of the 13 thematic categories. The figure below is a snapshot of what the data look like. As you can see it is just a 0/1 coding for each category indicating the respondent defined futility accordingly.
At this point, the fellow could have published the findings as a qualitative study, drawing in some key quotes from the respondents and visual inspection of the data (for example, maybe futility was defined consistently by provider role: e.g., nurse vs attending vs resident). But there is also an opportunity to use quantitative methods to answer a few important questions, strengthening the research:
- Are the qualitatively-defined 13 categories of futility correct?
- Do respondents define futility similarly by some common characteristic (provider role, age, years of experience, gender, etc.)?
There are several ways that qualitative and quantitative studies can inform each other in mixed methods analyses (a.k.a. multimethod analyses). One way is to use qualitative research to identify unknown confounders for a subsequent quantitative study. Another way is to test key assumptions or results of qualitative work by adding a statistical component. This work falls under the latter reason. What we don't want to do is use qualitative research to be redundant to the quantitative results, as the data are already captured in the quantitative analysis. The NIH publishes a set of best practices for mixed methods research in health science.
To address the two questions from earlier, we can turn to quantitative methods as follows:
- Are the qualitatively-defined 13 categories of futility correct?We need to know whether there is redundant or unneeded categories. A factor analysis (FA) will detect the correlations among variables and hopefully identify the most important classifiers of futility.
- Do respondents define futility similarly by some common characteristic (provider role, age, years of experience, gender, etc.)?We wish to group respondents based on similar definitions of futility. The grouping is a latent construct, not otherwise known to us, and can be ascertained via a latent class analysis (LCA). It's important to note that while we have the sociodemographic characteristics of the respondents in the data, we are not using the LCA to fit these data to the latent class, rather we blind ourselves to this knowledge, and have the LCA first define the categories, then we can describe them by similarity in terms of the characteristics.
This analysis can readily be accomplished using R, and specifically two functions: factanal (in the "stats" package) to perform the FA and poLCA (in the "poLCA" package) to perform the LCA. I am also just scraping the surface of each of these two techniques - the point is to introduce these concepts and their application, and not necessarily master them.
The factor analysis will essentially tell us which variables hang together in groups. The number of groups (or factors) is informed by statistics as well as interpretability. That is, just because a solution makes statistical sense it also needs to be interpretable. We'll focus on the following concepts in the input and output from factanal function:
- Factors: The number of factors under consideration. We have 13 predefined futility categories in our data. Perhaps several of these categories are redundant or maybe unnecessary. The factor analysis will help address this uncertainty.
- Loadings: I like to think of these as correlations between each variable (futility category) and a factor. Loadings will be bound between (-1, 1) and a loading of 0 means non-contributory (no correlation). A loading of -1 or +1 means a perfect correlation between the variable and a factor. The negative sign indicates the inverse from the expected correlation. In practice, many people use a threshold | loading | >= 0.5 to define a meaningful loading.
- Variance: The proportion variance tells you how much variance in the data is explained by a given factor (in general, the more the better), and the cumulative variance tells you the same thing but after considering all the factors (again, the more variance you are explaining, the better). But you also have to guard against overfitting the data - I can fit 13 factors to my 13 categories, explain all the variance, but I would also have a lot of factors that on their own explained 0 of the variance.
- P-value: A global goodness of fit test. A p-value that is non-significant (based on your alpha) says that you have sufficient number of factors, thus a significant p-value tells you that you may want to consider more factors in your analysis. Again though we want to focus on interpretability of your factors, and not just statistical mode fit.
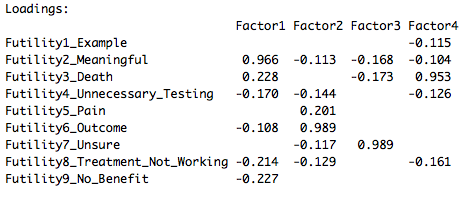
The factor analysis proceeds in an iterative fashion, adding or removing the number of factors, and possibility including or excluding some of the categories of futility if they are non-contributory in the overall data (i.e., unnecessary). It's an art. Results from my FA suggested a few things:
- The 13 categories appear excessive as some of the categories did not achieve any meaningful loading. I removed four of these categories.
- Among the remaining categories, the loadings were very high (|loading|>0.9) for a single variable under a given factor (see figure on right). This suggests to me that the categories defined from the qualitative data were thematically distinct: the fellow did a good job identifying the constructs!
- From the remaining nine categories fit into a four factor analysis, four of the categories appeared to drive the bulk of the definition of futility based upon the loadings.
- In conclusion, the factors generated did not uncover new information, but rather corroborated the qualitative interpretation of the data.
As mentioned, the LCA will group respondents together into latent classes based on similarity in defining futility. Informed by the factor analysis, I decided to omit the four categories that did not meaningfully contribute to the definition of futility. I also did not use the factors themselves as this did not yield new information (as assessed by the loadings being very high for a single variable under a given factor), rather I modeled the nine remaining futility categories. The following input and output can help drive the LCA:
- Classes: The number of latent classes under consideration. The ultimate goal of the LCA is to assess the alignment of the classes with the data, both statistically and theoretically.
- AIC/BIC: A global measure of model fit. Useful for comparing models (changing the number of classes). The smaller the value, the better the model fit.
- Entropy: I like to use relative entropy which is the measure produced by the software MPlus. The value ranges between 0 and 1, and indicates latent class overlap. As this number approaches 1, the latent classes are well-separated. As this number approaches 0 this is significant overlap in the classes. Combined with AIC/BIC these measures can help with statistical fit of the data.
- Class proportion: This measure is particularly useful for assessing the theory and interpretability of the LCA. For each of the nine categories of futility in the LCA (i.e., each covariate), we can assess its class membership.
As with the factor analysis, we proceed in an iterative fashion adding or removing latent classes from the LCA. We want not only statistical evidence for our model selection, but also a theoretical basis, meaning interpretability of the results. A difficult question to answer with is, "How many latent classes are appropriate for my data?" Some guidance is offered here. There are a variety of strategies to use, including model fit criteria (AIC/BIC) as well as class membership probabilities. Ultimately we chose a three class solution which optimized the BIC and entropy and did not result in excessive 0/1 probabilities: eventually the classes will become so unique that you lose the original intention of the LCA. The figure below demonstrates the class membership in our solution:
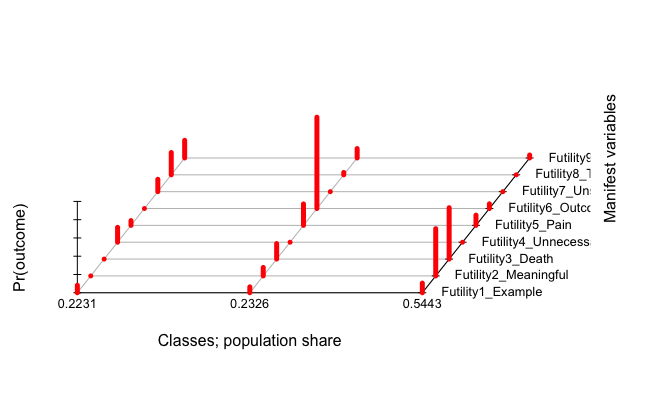
Latent class one (on left) seemed to define futility mainly by constructs 8 and 9; latent class two (middle) seemed to define futility by constructs 3, 5, 6; and latent class three (on right) seemed to define futility by constructs 2 and 3. One way to interpret this output is there are three general groups of individuals in the ICU who define futility in similar ways according to their class membership. Returning to the earlier question, "Do respondents define futility similarly by some common characteristic?", we can now assess class membership by the sociodemographic and worker characteristics, by joining the predicted class membership to the original survey data. Data can be inspected visually, by plotting graphs, or statistically, by assessing frequency tables. See below for proportional breakdown of latent class membership (y-axis) by provider role in the ICU (x-axis): attending physicians, fellows, residents, nurse practitioners, and nurses.
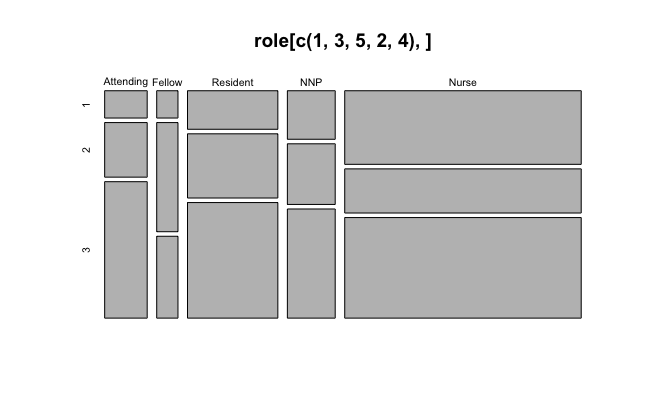
We tend to see attending physicians and fellows were least likely to define futility according to the latent class one constructs, while nurses were least likely to define futility according to the latent class two constructs. We can also compare and contrast provider role differences by latent class membership.
Cite: Goldstein ND. An exploratory mixed methods study using factor analysis and latent class analysis. Nov 22, 2017. DOI: 10.17918/goldsteinepi.